曲线拟合、回归模型介绍

一、直线拟合回归方程：

    直线回归是最简单的回归模型,也是最基本的曲线拟合回归分析方法， 将所有的测试点拟合为一条直线，其拟合函数方程式为：y=a+bx

二、二次多项式拟合回归方程：

    二次多项式成抛物线状，开口向下或者向上，在很多ELISA实验中，拟合近似于二次多项式的升段或者降段，由于曲线的特性，同一个浓度值在曲线图上可能表现出没有对应的OD值、有一个OD值，或者两个OD值，所以使用二次多项式拟合时，最好保证取值的范围都落在曲线的升段或者降段，否则哪怕是相关系数很好也很可能与实际的值不一致。其拟合函数方程式为：y = a + b x + c x² ，形状如下图：

三、三次多项式拟合回归方程：

    三次多项式像倒状的‘S’形，在实验结果刚好在曲线的升段或者降段的时候，效果还可以，但是对于区间较广的情形, 由于其弯曲的波动，三次方程拟合模拟不一定很好.跟二次方程拟合一样，看曲线的相关系数的同时也要看计算的点在曲线上的分布，这样才算出理想的结果，本软件计算值时，选择性的取相对于浓度或者OD值，比较符合实际的那个结果，而没有将多个结果列出。拟合函数方程式为：y = a + b x + c x² + d x³ ，形状如下图：

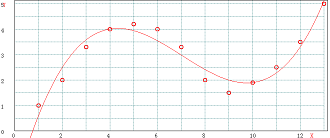
四、半对数拟合回归方程：

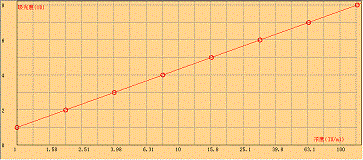
    半对数拟合即将浓度值取对数值，然后再和对应的OD值进行直线回归，理想的状态下，在半对数坐标中是一条直线，常用于浓度随着OD值的增加或者减低呈对数增加或者减少的情况，即浓度的变化比OD值的变化更为剧烈。在ELISA实验中较常用（有很多用EXCEL画图时，也常使用半对数），拟合函数方程式为：y = a lg(x) + b ，形状如下图(注意其X轴是对数坐标)：

五、Log-Log拟合回归方程：

    Log-Log拟合和半对数相似,只是将OD值和对应的浓度值均取对数，然后再进行直线回归，拟合函数方程式为：lg(y) = a lg(x) + b ，形状如下图：

六、Logit-log 直线回归方程：

    Logit-log则是免疫学检测中的模型, 可用于竞争法。它最早用于 RIA， 但在 ELISA 中也是可以应用的。 Logit 变换源于数学中的 Logistic 曲线。在竞争法放射免疫分析(RIA) 及 ELISA 中，当竞争性反应物为 0 时结合率为 100%， 如果某一浓度下结合率为 B，B=OD/OD(0)，在对B进行 Logit 变换：y=ln[B/(1-B)]，之后y与浓度的对数成线性关系，即：y = a + b lg(x)，拟合函数方程式为：lg(y) = a lg(x) + b 就得到了Logit-log 直线回归模型，这个模型一般适用于竞争法的拟合，所以拟合时要求只有少有一个零浓度测试的OD值，并且此值为整个反应的最大值(也就是我们常说的至少要做一个空白对照)。

七、四参数拟合回归方程：

    四参数方程的拟合函数表达式为：

    它不仅限于竞争法, 实际上夹心法也可以用它。它的形状, 根据情况, 可能是一个单调上升的类似指数, 对数, 或双曲线的曲线, 也可能是一个单调下降的上述曲线, 还可以是一条 S 形曲线。 它要求 X 值不能小于0 (因为指数是实数, 故有此要求)。 在很多情况下它都可以拟合 ELISA 的反应曲线, 所以它也成了 ELISA 中应用最广的模型之一。

八、三次样条插值：

    早期工程师制图时，把富有弹性的细长木条（所谓样条）用压铁固定在样点上，在其他地方让它自由弯曲，然后沿木条画下曲线。成为样条曲线，三次样条插值（简称Spline插值）是通过一系列形值点的一条光滑曲线，数学上通过求解三弯矩方程组得出曲线函数组的过程。所以三次样条插值实际上各个测试点间的每一段都是一个三次方程的拟合函数，并对两端都进行平滑处理，得到的一组三次方程组。本软件的算法中的边界条件取的是自然边界（即边界点的导数为0,)这样处理出来的曲线更符合ELISA的实验结果，在数据点较多时，其拟合的效果也和实际结果非常吻合。现在有些自动化的分析仪器中，比如某些型号的全自动化学发光分析仪，计算结果就是使用三次样条插值进行结果的处理的。。

九、点对点拟合计算：

    顾名思义，点对点就是将测试点画在坐标上，然后依次用直线连起来，每一段都是一个直线方程，总的来说就是得到一直线方程组，然后依照浓度或者OD值，求出其在某一段直线上的OD值或者浓度值，是一种较为粗糙的拟合方法，在数据较为密集时结果还算可以。

十、应用选择：

    在实验过程中，要根据各个实验本身的特点，选择最适合的曲线拟合模型，才能得到最合理的实验结果。

相关文章

  1、 酶联免疫吸附试验(ELISA)曲线拟合小软件

  2、 酶联免疫吸附试验(ELISA)曲线拟合小软件使用说明

  3、 在线曲线拟合